Astronomie.me

Berechnungen

Wie groß muss der Sensor unserer Kamera sein, damit der Mond vollständig abgebildet wird?

Anpassung der Brennweite an die Pixelgröße der Kamera

Auflösung Teleskop

Auflösung des Teleskops messen

Kann man auf dem Mond die Landefähren sehen?

Keine Angst- ich möchte hier keine Berechnungen von Planetenkonstellationen eines bestimmten Tages o.ä. vorstellen. Das das sehr reizvoll sein kann ist unbestritten. Ich benutze dazu lieber meine Planetarium-Programme- nebenbei muss ich mich auch noch um andere Dinge kümmern. Hier geht es um praktische Beispiele, die man für das Astro-Hobby benötigt.

Als Anfang der 70er Jahre die Taschenrechner für Normalverdiener erschwinglich wurden, tat sich für mich eine ganz neue Welt auf. Bis zu diesem Zeitpunkt musste ich meine Berechnungen immer mit Tabellenbüchern und Rechenschieber machen. Alleine der Zeitgewinn war enorm und Rechenfehler gehörten auch der Vergangenheit an. Es hat richtig Spaß gemacht die unterschiedlichsten Aufgaben zu Berechnen. In der Astronomie muss man öfter mit sehr kleinen Winkeln rechnen, das war damals mit den Tabellenbüchern nicht möglich. Ich möchte hier ein paar Beispiele zeigen, die einem das Astro-Hobby sehr erleichtern können. Dazu benötigt man nur paar Formeln und einen Taschenrechner (möglichst mit Winkelfunktionen). Ich benutze den Taschenrechner HiPER Calc Pro auf dem Smartphone, mit dem ich sehr zufrieden bin.

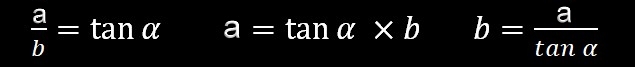
Mit den Winkelfunktionen können wir viele Aufgaben lösen, die wir sonst nur umständlich ermitteln müssten. Fangen wir einfach mal an.

Wir möchten den Mond mit unserem Teleskop fotografieren. Wie groß muss der Sensor unserer Kamera sein, damit der Mond vollständig abgebildet wird?

Gegeben:

• Brennweite des Teleskops (z.B. 1200mm)
• Durchmesser Mond 3474.8 km
• Entfernung Mond 385000 km (mittlere Entfernung)

Zuerst müssen wir den Sehwinkel berechnen, der Winkel, unter dem wir den Mond sehen. Wir nehmen für den

• Mond = a
• Entfernung = b

tan α = a/b
tan α = 3474.8 / 385000 = 0.009025
tan α = 0.009025
Der Tangens gibt das Verhältnis von a/b an, das immer einem bestimmten Winkel entspricht. Früher musste man im Tabellenbuch nachsehen, welcher Winkel dem Tan α = 0.009025 entspricht. Heute nehmen wir einfach den Taschenrechner und benutzen die Tan-Umkehrfunktion:
tan -¹ 0.009025 = 0,517106°
oder in Grad Minuten Sekunden ausgedrückt:
tan -¹ 0.009025 = 0° 31' 1.58"
Wir sehen den Mond unter einem Sehwinkel von 0° 31' 1.58"
Für die Sensorgröße a müssen wir die Formel jetzt umstellen:
a = tan α x b

• α = 0° 31' 1.58" (Sehwinkel)
• b = Brennweite des Teleskops 1200mm

tan α 0° 31' 1.58" = 0.009025
a = 0.009025 x 1200mm = 10,831mm
Um den ganzen Mond mit einer Brennweite von 1200mm abzulichten müsste der Sensor eine Größe von 10,831x10.831mm haben.
Überprüfen können wir das mit einem Planetarium-Programm, z.B. Stellarium. Wir geben die Sensorgröße und die Brennweite des Teleskops ein und erhalten das Ergebnis grafisch angezeigt

Auflösung Teleskop

Welche kleinsten Krater kann ich mit einem Teleskop noch auflösen?
Zuerst müssen wir wissen, welche Auflösung unser Teleskop hat.

• Beispiel: Teleskop Objektivdurchmesser 100mm Brennweite 1200mm

Eine einfache Faustformel lautet:
Auflösung α (in Bogensekunden ") = 122 / Objektivdurchmesser (in mm)
α = 122 / 100 = 1,22"
Das Teleskop hat eine Auflösung von 1,22"

Nun müssen wir wieder mit dem Tangens rechnen.
Gegeben ist der Winkel (Auflösung Teleskop) und die Entfernung zum Mond.

• α Auflösung 1.22"
• b Entfernung Mond 385000 km (mittlere Entfernung)

Gesucht wird der Wert a (Kratergröße). Nach der obigen Formel
a = tan α x b
tan 0°0'1.22" = 0.000005914726909
a = tan α x b
a = 0.000005914726909 x 385000 km = 2,277 km
Wenn der Taschenrechner nicht mit Grad/Minuten/Sekunden rechnen kann, muss man Bogensekunden in Dezimalgrad umrechnen und dann den Tangens ermitteln:
1.22" / 3600 = 0,000338888888°
tan 0,000338888888° = 0.000005914726909
a = tan α x b
a = 0.000005914726909 x 385000 km = 2,277 km
mit unserem Teleskop können wir Krater mit einem Durchmesser von 2.277km auflösen.

Kann man auf dem Mond die Landefähren sehen?

Ich werde ab und zu mal gefragt, wenn ich mit den großen Teleskopen auf der Terrasse bin, ob man die Landefähren auf dem Mond sehen kann, meist natürlich zum Spaß. Wenn ich dann antworte "ja, natürlich" gibt es immer große Augen. "Aber nicht von der Erde aus".
Das hat zwei Gründe:

1. Gibt es nicht so große Teleskope und
2. Macht unsere Atmosphäre so eine Beobachtung unmöglich

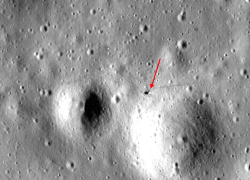
Um die Mondoberfläche genau zu Kartieren wurden Satteliten gebaut, die den Mond in geringer Höhe umkreisen und hoch aufgelöste Aufnahmen machen. Auf diesen Aufnahmen sind die Landefähren zu erkennen. Folgende Aufnahmen wurden mit dem LROC gemacht:

Apollo 11	Apollo 12	Apollo 17

Wir rechnen mal schnell aus, wie groß ein Teleskop theoretisch sein müsste, um eine ca. 10m große Landefähre aufzulösen.
Gegeben ist die Größe der Landefähre auf dem Mond und die Entfernung zum Mond.

• a Landefähre 10m
• Entfernung zum Mond 385000km

Zuerst müssen wir den Sehwinkel berechnen.
tan α = a/b
tan α = 0.010 / 385000 = 0.00000002597402
tan α = 0.00000002597402
tan -¹ 0.00000002597402 = 0°00'0.00538"
Der Teleskop-Spiegel müsste eine Auflösung von 0°00'0.00538" haben
Nun müssen wir die Formel für die Auflösung umstellen

D = 122 / α (Ergebnis in mm)
D = 122 / 0.00536" = 22677mm = 22.677m
 Der Teleskop-Spiegel müsste einen Durchmesser von 22.677m haben.

Wir möchten die Auflösung unseres Teleskops messen

Unser Teleskop hat einen Objektiv-Durchmesser von 100mm
Wir haben einen Blatt Millimeter
Unser Objektiv hat eine Auflösung von 122 / 100 = 1.22"
Wie weit muss das Blatt Millimeterpapier entfernt sein, damit der Abstand von Millimeter zu Millimeter einem Winkel von 1.22" entspricht?

• Gegeben Sehwinkel 1.22"
• Gegeben Abstand a = 1mm
• tan 0°0'1.22" = 0.000005914726909
  

Gesucht wird die Entfernung b, bei dem der Abstand a (1mm) einem Winkel von 1.22" entspricht.

b = 1 / 0.000005914726909 = 169069.56mm = 169.069m
Wir müssen unser Blatt Millimeterpapier 169.069m entfernt platzieren, damit 1 Millimeter-Abstand 1.22" entspricht.
Da bekommt man einmal ein Gefühl, wie klein der Winkel einer Bogensekunde ist.
Ich teste die Auflösung meiner Optiken natürlich nicht mit Millimeterpapier.
Zu diesem Zweck gibt es extra dafür gemachte Testplatten.
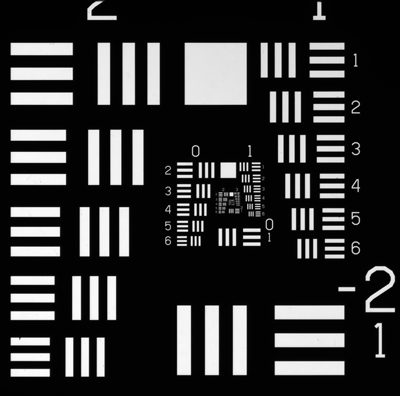
Ich benutze das sogenannte USAF-1951 Standard Resolution Target.

Die Abstände der Balken unterliegen einer mathematischen Formel. Somit kann man schnell die Auflösung anhand der noch aufgelösten Gruppe bestimmen. Mein Test Target geht noch bis Gruppe 7 Element 6 entsprechend einer Auflösung von 228.1 Linien / mm (Linien-Abstand 0,00438mm).

Anpassung der Brennweite an die Pixelgröße der Kamera

In den Astronomie-Foren im Internet werden immer wieder Fragen nach der Pixelgröße der Kamera bzw. die Anpassung der Brennweite daran gestellt. Dann heißt es meist: Nimm die Pixelgröße der Kamera mal Faktor 3 für SW und für Farbchips etwa mal Faktor 5 dann hat man das nötige Öffnungsverhältnis.
Wenn man dann einmal nachfragt heißt es: Damit das Nyquist-Kriterium erfüllt wird oder das Rayleigh-Kriterium. Kurz gesagt, ob und wie man z.B. zwei Sterne noch auflösen (trennen) kann.
Grundsätzlich: Die Auflösung von einem Objektiv ist nur von dem Durchmesser abhängig. Bei großer Öffnung (Durchmesser Objektiv) und kleiner Brennweite kann man die Auflösung nicht nutzen, wenn die Pixel auf dem Kamerachip zu groß sind. Aus diesem Grunde muss man die Brennweite an die Pixelgröße anpassen. Bei den heutigen modernen Kameras kann man sich die Rechnerei bei Mond und Planetenaufnahmen fast sparen.

Wir rechnen mal wieder

• Gegeben Teleskop 152 / 1200
• Auflösung 0,8" (122 / 152 = 0,8)
• tan 0,8" = 0.000003878509
• Pixelgröße Kamera 2.4µm

Gesucht wird die Größe des Beugungsscheibchens auf dem Kamera Chip

a = tan α x b
a = 0.000003878509 x 1200
a = 0.00465 = 4.65µm
Wir benötigen zur Trennung von zwei Objekten (Sternen) mit einem Abstand von 0.8" auf dem Kamera-Chip mindestens 2 Pixel mit der halben Größe des Beugungsscheibchens.
4.65µm / 2 = 2.325µm
Mit der 2.4µm Pixelgröße der Kamera kommen wir also gut zurecht.

Mit der Faustformel weiter oben gerechnet für eine Mono Kamera
Gesucht wird das Öffnungsverhältnis (Brennweite zu Öffnung)

Pixelgröße Kamera 2.4µm x 3 = 7.2
Das Öffnungsverhältnis des Teleskops sollte als mindestens 7,2 haben.
Das Teleskop 152 / 1200 hat ein Öffnungsverhältnis von
1200 / 152 = 1/7. 89
passt also auch.
Mann sollte daraus aber keine Doktorarbeit machen. Die Übergänge sind nicht so scharf abgegrenzt, wie man es sich vielleicht vorstellt.

Dazu mal ein Beispiel aus der Praxis:
Mein Teleskop 152 / 1200 hat eine Auflösung von 0,8"
In meinem Optik-Messraum habe ich ausgerechnet, das ich mit dem Abstand zur Testplatte die Gruppe 4 Element 2 = Abstand 0.0556mm noch auflösen kann. Das Ergebnis zeigte aber die Gruppe 4 Element 4, was einer Auflösung von 0,0442mm entspricht oder 0,685"